Hash tables are a common data structure for storing key-value pairs.
To get a better understanding of how they work I started building my own data structure to store key-value pairs and then tried to optimize it for performance.
If you’ve got the time, consider trying to come up with your own solutions before reading on.
The goal
Hash tables can be used to implement associative arrays (also called dictionaries). This is how our hash table will work:
var dict = new HashTable();
dict.set("PI", 3.14)
dict.get("PI") // ==> 3.14A naive key-value store
Let’s start with a very naive implementation of a dictionary. We’ll actually end up using this in our hash table later on too.
function NaiveDict(){
this.keys = []
this.values = []
}
NaiveDict.prototype.set = function(key, value){
this.keys.push(key)
this.values.push(value)
}
NaiveDict.prototype.get = function(lookupKey){
for (var i=0;i<this.keys.length;i++){
var key = this.keys[i];
if (key === lookupKey) {
return this.values[i]
}
}
}NaiveDict does everything we set out to do, but it’s very slow. We may need to iterate through every item in the table, so worst-case performance is O(n).
How hash tables work
At the core of a hash table is an array of roughly similar size to the number of key-value pairs stored in the hash table.
Each index in the array is called a bucket (or entry, or slot) and stores any number of key-value pairs. A bucket may not have any key-value pairs in it, or all key-value pairs in the hash table may be in the same bucket. But the goal is to equally distribute key-value pairs across the buckets.
The key of a key-value pair decides what bucket it should be stored in. First, the key is converted to a number using a hash function:
var hash = hashFunction("PI") // => 127,872We want to use the hash as an index in our array of buckets. But what if we only have 1000 buckets, and the hash value exceeds the array size?
To solve that problem we use the modulo operator to get an index that’s smaller than our array size.
var arraySize = 1000
var bucketIndex = hash % arraySizeSometimes the hash function will return the same hash for the same key – that’s called a collision.
Because collisions are possible we need a second level of storage in each bucket. In this example we’ll use the NaiveDict class from above.
When initializing the hash table we create an array containing a fixed number of these buckets.
More complex hash table implementations will resize the table dynamically based on the number of items they store.
function HashTable(){
this.bucketCount = 100000;
this.buckets = [];
for (var i=0; i< this.bucketCount;i++){
this.buckets.push(new NaiveDict())
}
}We need to decide how our hash function should work. For now, let’s use a very simple implementation that takes the sum of the ASCII codes of the characters in the key.
HashTable.prototype.hashFunction = function(key){
var hash = 0;
for (var i=0;i< key.length;i++){
hash += key.charCodeAt(i)
}
return hash;
}To determine the correct bucket given a certain key we use the modulo operator on the hash of the key, then retrieve the bucket at the index we just calculated.
HashTable.prototype.getBucketIndex = function(key){
return this.hashFunction(key) % this.bucketCount
}
HashTable.prototype.getBucket = function(key){
return this.buckets[this.getBucketIndex(key)]
}Finally, we implement the get and set functions. Each bucket contains a NaiveDict, so we can insert or look up the key there.
HashTable.prototype.set = function(key, value){
this.getBucket(key).set(key, value)
}
HashTable.prototype.get = function(lookupKey){
return this.getBucket(lookupKey).get(lookupKey)
}We’ve got a working hash table!
Measuring performance
Let’s see how well our hash table is doing.
This test generates 100,000 keys and values, then measures how long it takes to insert (SET) and then read (GET) them from the hash table.
I took the makeid function from StackOverflow.
We use console.time and console.timeEnd to measure how fast our hash table is.
var dict = new HashTable();
var keys = []
var values = []
for (var i = 0;i< 100000;i++){
keys.push(makeid())
values.push(Math.round())
}
console.time("SET")
for (var i = 0;i < keys.length;i++){
dict.set(keys[i], values[i])
}
console.timeEnd("SET")
console.time("GET")
for (var i = 0;i < keys.length;i++){
var val = dict.get(keys[i])
}
console.timeEnd("GET")Result on my machine:
SET: 108.112ms
GET: 760.709ms
That’s pretty good! Doing the same test with NaiveDict takes almost two minutes:
SET: 7.021ms
GET: 111172.771ms
I also tried wrapping a native JavaScript object with a get and set function:
SET: 127.702ms
GET: 30.727ms
Let’s see if we can get the performance of our hash table closer to that.
A better hash function
I mentioned earlier that, ideally, the hash function should uniformly distribute keys to buckets. But here’s what our hash function does:
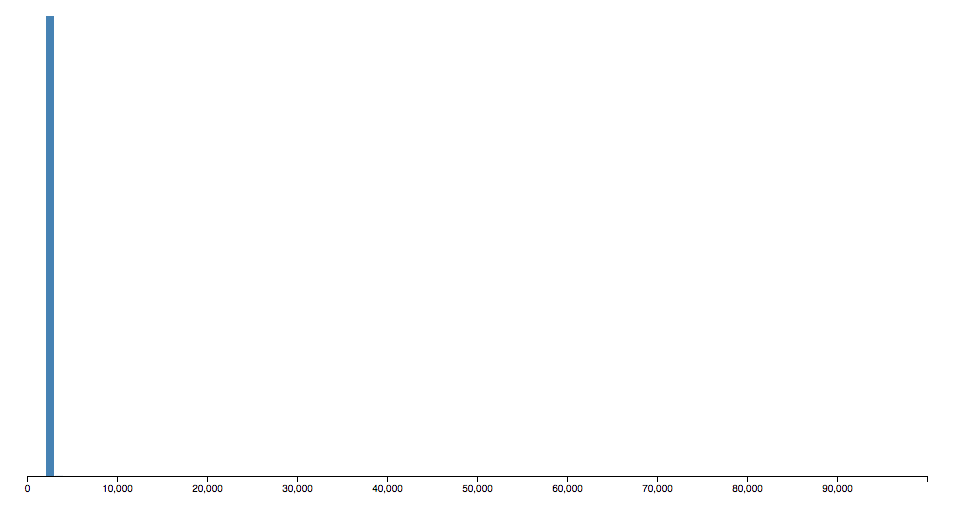
Only a few hundred buckets are actually used.
The current hash function treats every character equally, but let’s change it to take the position of the character into account:
HashTable.prototype.hashFunction = function(key){
var hash = 0;
for (var i=0;i< key.length;i++){
hash += key.charCodeAt(i) * i
}
return hash;
}Now a bit over 10 thousand buckets are used:

And we get better performance:
SET: 208.314ms
GET: 95.843ms
Still, it’s not a perfectly uniform distribution. I’m too lazy to think about how to achieve that, but conveniently Mark Wilbur already wrote a blog post about hash tables in JavaScript, and this is the hash function he uses:
HashTable.prototype.hashFunction = function(key){
var hash = 0;
if (key.length == 0) return hash;
for (var i = 0; i < key.length; i++) {
hash = (hash<<5) - hash;
hash = hash + key.charCodeAt(i);
hash = hash & hash; // Convert to 32bit integer
}
return Math.abs(hash);
}Which uses most of the buckets we’ve allocated!
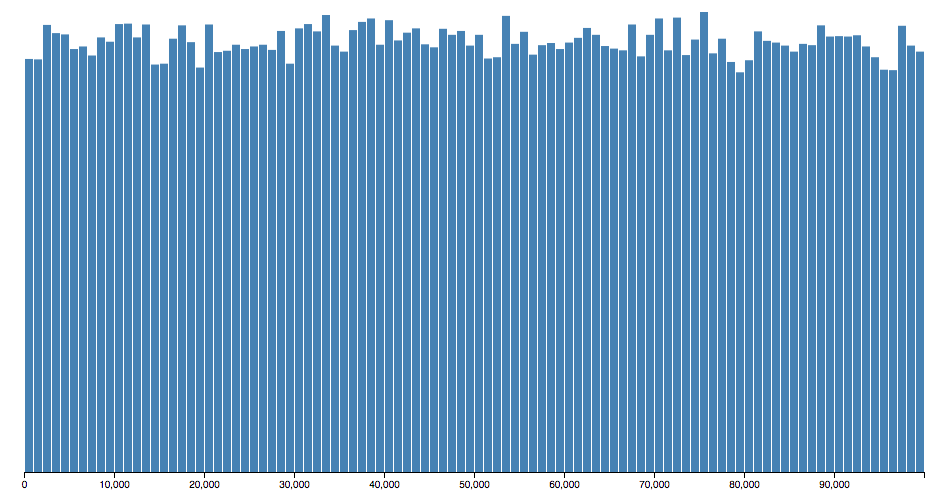
However, this hash function is also more complicated and takes more time to run. That makes inserting the key-value pairs take longer. But because we have fewer collisions retrieval becomes faster, despite the increase in time spent on hashing.
SET: 434.148ms
GET: 72.455ms
More things we could do better
While our CPU performance is pretty good there’s still a lot of room to save on memory. For example, even buckets that contain no items currently use up memory (two empty lists in NaiveDict).
Also, in practice the individual buckets often use linked lists rather than our NaiveDict. I’m not sure that would do much for performance, but it might reduce memory consumption as normal JavaScript lists may take up more memory than necessary in order to be able to grow, while linked lists can be more efficient.
While we can retrieve the correct bucket in constant time (O(1)), the complexity of retrieving the value from NaiveDict is still O(n).
However, now our n is much smaller. In fact, if our hashes were perfectly distributed and there are no collisions each NaiveDict would only contain one item. Thus, in the best case O(n) becomes O(1)!.
